The Twofish Encryption Algorithm
Dr. Dobb's Journal, December 1998.
In 1997, the National Institute of Standards and Technology (NIST) called for the replacement of the DES encryption algorithm. Fifteen candidates came forward. The selection process will take about two years. (For more information on the process, see the accompanying text boxes entitled "The History of AES" and "The AES Candidates.") Twofish is our submission.
John Kelsey, Chris Hall, Niels Ferguson, David Wagner, Doug Whiting, and I designed Twofish to be fast, flexible, and secure. It’s conservative—there are no radical new security ideas or design elements. And it’s completely free—there are no patent royalties on the algorithm, copyright on the code, or license fees on anything. We have not applied for a patent on Twofish, and have no plans to do so.
Twofish
Twofish is a symmetric block cipher; a single key is used for encryption and decryption. Twofish has a block size of 128 bits, and accepts a key of any length up to 256 bits. (NIST required the algorithm to accept 128-, 192-, and 256-bit keys.) Twofish is fast on both 32-bit and 8-bit CPUs (smart cards, embedded chips, and the like), and in hardware. And it’s flexible; it can be used in network applications where keys are changed frequently and in applications where there is little or no RAM and ROM available.
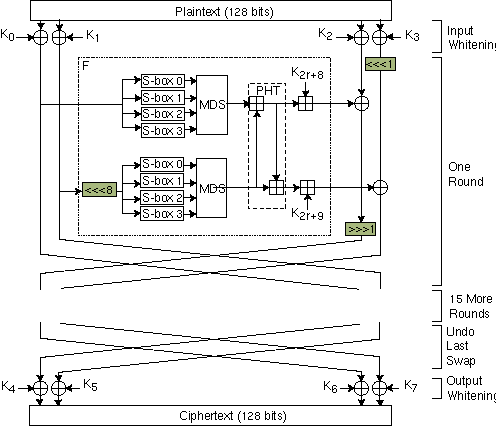
Figure 1
As Figure 1 illustrates, Twofish is a Feistel network. This means that in each round, half of the text block is sent through an F function, and then XORed with the other half of the text block. DES is a Feistel network. Blowfish (another Schneier algorithm) is a Feistel network. Five of the AES submissions are Feistel networks. Feistel networks have long been studied in cryptography, and we know how they work.
In each round of Twofish, two 32-bit words (the two vertical lines along the left of Figure 1) serve as input into the F function. Each word is broken up into four bytes. Those four bytes are sent through four different key-dependent S-boxes. The four output bytes (the S-boxes have 8-bit input and output) are combined using a Maximum Distance Separable (MDS) matrix and combined into a 32-bit word. Then the two 32-bit words are combined using a Pseudo-Hadamard Transform (PHT), added to two round subkeys, then XORed with the right half of the text. There are also two 1-bit rotations going on, one before and one after the XOR. Twofish also has something called "prewhitening" and "postwhitening;" additional subkeys are XORed into the text block both before the first round and after the last round.
The algorithm might look haphazard, but we did everything for a reason. Nothing is in Twofish by chance. Anything in the algorithm that we couldn’t justify, we removed. The result is a lean, mean algorithm that is strong and conceptually simple.
Each step of the round function is bijective. That is, every output is possible. We’ve seen too many attacks against ciphers that don’t have this property not to include it. The round function mixes up operations from different algebraic groups: S-box substitution, an MDS matrix in GF(28), addition in GF(232), addition in GF(2) (also called XOR), and 1-bit rotations. This makes the algorithm difficult to attack mathematically.
The key-dependent S-boxes are designed to be resistant against the two big attacks of the early 1990s—differential cryptanalysis and linear cryptanalysis—and resistant against whatever unknown attacks come next. Too many algorithm designers optimize their designs against specific attacks, without thinking about resistance against the unknown. Our design philosophy was a bit different: good enough against known attacks, and enough nastiness to (hopefully) resist unknown attacks. Key-dependent S-boxes were one way we did that.
Key-dependent S-boxes were not selected randomly, as they were in Blowfish. Instead, we carefully designed S-box construction rules, and tested them with all possible 128-bit keys (and a subset of possible longer keys) to make sure that all the S-boxes were indeed strong. This approach allowed us to combine the strength of fixed, strong S-boxes with the strength of secret S-boxes. And Twofish has no weak keys, as Blowfish does in reduced-round variants.
The MDS matrix was carefully chosen to provide good diffusion, to retain its MDS property even after the 1-bit rotation, and to be fast in both hardware and software. This means that we had to search through all possible matrices and find the one that best met our criteria.
The PHT and key addition provide diffusion between the subblocks and the key. And using the LEA instruction on the Pentium (and above), we can do all four additions in just two operations.
The round subkeys are carefully calculated, using a mechanism similar to the S-box construction rules, to prevent related-key attacks and to provide good key mixing. One of the things we learned during this process is that a good key schedule is not grafted onto a cipher, but designed in tandem with the cipher. We spent a lot of time on the Twofish key schedule, and are proud of the results.
The 1-bit rotation is designed to break up the byte structure; without it, everything operates on bytes. This operation exists to frustrate cryptanalysts; it certainly frustrated our attempts at cryptanalyzing Twofish.
The prewhitening and postwhitening seems to add at least a round to the difficulty of any attack. Since eight XORs are cheaper than a round, it makes sense to leave them in.
Twofish’s Performance
Twofish screams on high-end CPUs, and it’s flexible enough for tiny smart-card CPUs. It also works well in hardware. And there are several performance trade-offs between key-setup time and encryption speed that make it unique among the AES candidates.
Almost all encryption algorithms have some kind of key-setup routine: a way to take the key and make the round subkeys that the algorithm uses. Twofish needs to take the key and make key-dependent S-boxes and round subkeys. Blowfish, which needed to do the same thing, was slow in setting up a key, taking as long as 521 encryptions. Twofish is much faster; its key setup can be as fast as 1.5 encryptions.
Twofish has a variety of options. You can take longer for key setup and the encryption runs faster; this makes sense for encrypting large amounts of plaintext with the same key. You can setup the key quickly and encryption is slower; this makes sense for encrypting a series of short blocks with rapidly changing keys. Table 1 shows the performance of key setup and encryption, in clock cycles per block, for five keying options on both the Pentium II/Pentium Pro and Pentium, in assembly language.

Table 1: Twofish performance of key setup and encryption.
Other processors are similar or better. In general, the Intel architecture is the most annoying, and the hardest to optimize. It is far easier to write code that meets these performance numbers on a more general architecture, say the UltraSparc, 68040, or G3.
All of these options interoperate; they are just different ways of implementing the same Twofish algorithm. Data can be encrypted using one option and decrypted with another.
On smart cards, Twofish also has a variety of trade-offs. Table 2 is based on code written for a 6805 CPU. The RAM estimates assume that the key must be stored in RAM. If the key can be stored in EEPROM, then the algorithm only needs 36 bytes of RAM to run. The code size includes both encryption and decryption code. If only encryption has to be implemented, the code size and speed numbers improve somewhat.

Table 2: Twofish smart-card performance based on code written for a 6805 CPU.
Key setup on this processor is about 1750 clocks per key, which can be cut considerably at the cost of two additional 512-byte ROM tables. And the 6805’s lack of a second index register has a significant impact on the code size and performance of Twofish; a CPU with multiple index registers (the 6502, for instance) will be a better fit for the algorithm.
These estimates are for a 128-bit key. For larger keys, the extra code size is negligible: less than 100 bytes for a 192-bit key, and less than 200 bytes for a 256-bit key. The encryption time increases by less than 2600 clocks for a 192-bit key, and about 5200 clocks for a 256-bit key. Similarly, the key schedule precomputation increases to 2550 clocks for a 192-bit key, and to 3400 clocks for a 256-bit key.
It’s possible to shrink Twofish even further, saving about 350 bytes of ROM while decreasing performance by a factor of 10 or more. This is only useful in limited situations, but it shows how flexible the algorithm really is.
Similar sorts of trade-offs exist when putting the algorithm into hardware: key setup speed, for example, versus encryption speed, or speed versus gate count.
Cryptanalysis of Twofish
We spent over 1000 man-hours cryptanalyzing Twofish. The detailed results are in the Twofish design document (http://www .counterpane.com/twofish.html), but here are the highlights.
Our best attack works against five rounds of Twofish, without the prewhitening and postwhitening. It requires 222.5 chosen plaintext pairs and 251 work. We expect further research and clever techniques will extend this attack a few more rounds, but don’t believe that there are any attacks against more than nine or 10 rounds.
We also have a related-key attack. It’s a partial chosen-key attack on 10 rounds of Twofish without the prewhitening and postwhitening. To mount the attack, we have a pair of related keys. We get to choose 20 of the 32 bytes of each key. We have complete control over those 20 bytes of both keys. We don’t know the remaining 12 bytes of key, but we do know that they are the same for both keys. We end up trying about 264 chosen plaintexts under each key, and doing about 234 work, to recover the remaining unknown 12 bytes of key. No, it’s not a terribly realistic attack, but it’s the best we can do.
And we have reduced-round attacks on simplified variants: Twofish with fixed S-boxes, Twofish without the 1-bit rotations, and so on. We can’t break full Twofish even with these simplifications, but our analysis helps us understand why those components are there and what they are doing.
Of course, with any encryption algorithm, it’s "buyer beware." As a designer of Twofish, I am the least qualified to make pronouncements about its security. As the AES process continues, and other cryptographers start analyzing Twofish, we hope to collect evidence of its security. Until then, it’s best to wait.
Conclusion
We feel that Twofish is the best choice among all the AES candidates because of its unique combination of speed, flexibility, and conservative design. Assuming it’s secure (and only time will tell), Twofish is the fastest AES candidate across all CPUs. Twofish fits on smart cards, even those that only have a couple of registers, a few bytes of RAM, and little ROM. And it fits in hardware in few gates.
No other algorithm has the same flexibility in implementation: the ability to trade off key-setup time for encryption speed, and ROM and RAM for encryption speed. These options exist on 32-bit CPUs, 8-bit CPUs, and hardware.
And Twofish does this with a conservative design. We chose not to modify the basic Feistel network. We did not use data-dependent rotations, 32-bit multiplies, or any other poorly understood primitives. The key schedule is designed to resist even the nastiest of attacks. And we gave the cipher 16 rounds when we could only break five.
Reference code and executables that implement and test Twofish are available electronically (see "Resource Center," page 3). The files include platform-specific definitions, macros, and tables for Twofish internal structures, reference ANSI C source code, test code, an executable 32-bit console app of TST2FISH.C and TWOFISH.C, and the like.
The Twofish web site (http://www .counterpane.com/twofish.html) has the Twofish design document, free source code in a variety of languages for a variety of platforms, and any late-breaking news. Readers outside the U.S. and Canada can go to the web site to find pointers to Twofish code on servers outside the U.S.
Sidebar: The History of AES
In 1972 and 1974, the National Bureau of Standards (now the National Institute of Standards and Technology, or NIST) issued the first public request for an encryption algorithm for its new encryption standard. IBM submitted an algorithm that would become DES, arguably the most widely used and successful encryption algorithm in the world.
Despite its popularity, DES has been plagued with controversy. Some cryptographers objected to the closed-door design process of the algorithm, and wondered whether the NSA added a trap door to allow surreptitiously breaking the algorithm. The 56-bit key was viewed by some as too short; certainly it is insufficient for today’s security applications.
There are other choices, including IDEA, Blowfish, RC5, and CAST-128. Triple-DES has emerged as an interim solution for banking and other conservative systems, but it is too slow for some uses. (DES was designed when 4-bit components were the norm, and it shows.) More fundamentally, the 64-bit block length shared by DES and most other trusted ciphers opens it up to attacks when large amounts of data are encrypted under the same key. And none of the other choices is a standard in the way that DES is.
In response to a growing desire to replace DES, NIST announced the Advanced Encryption Standard (AES) program in January 1997 (http://www.nist.gov/aes/). Submissions were due in June 1998, and the 15 submitters presented their algorithms to the world in August at the First AES Candidate Conference. NIST will hold a Second AES Candidate Conference in Rome next March, and will accept public comment on the algorithms until June 15, 1999. It will choose approximately five finalists, solicit another round of public comment, hold a third AES Candidate Conference around January 2000, then choose a winner. Then NIST will make it into a Federal Information Processing Standard.
Think of the process as a cryptographic demolition derby. Everyone submits their algorithms into the ring, then attacks all others while defending their own. The crowd votes for the winner among those left standing at the end. Bloody, yes, but not a bad way to pick an industry standard encryption algorithm.
NIST’s call was for a block cipher. Block ciphers can be used to design stream ciphers with a variety of synchronization and error-extension properties, one-way hash functions, message-authentication codes, and pseudorandom number generators. Because of this flexibility, they are the workhorses of modern cryptography.
NIST specified several other design criteria: a longer key length, larger block size, faster speed, and greater flexibility. While no single algorithm can be optimized for all needs, NIST intends AES to become the standard symmetric algorithm of the next several decades.
Sidebar: The Current State of DES
DES is the Data Encryption Standard, the current standard encryption algorithm. On July 17, 1998 the Electronic Frontier Foundation (EFF) announced the construction of a DES brute-force hardware cracker (http://www.eff.org/ descracker/). This $220,000 device can break a DES key in an average of 4.5 days.
The news here is not that DES is insecure, that hardware algorithm-crackers can be built, nor that a 56-bit key length is too short; cryptographers have been saying it for years. Technological predictions made about the declining costs of such a machine, made in the late 1970s, the 1980s, and the early 1990s, turned out to be dead-on.
The news is how long the government has been denying that these machines were possible. As recently as June 8, 1998, Robert Litt, principal associate deputy attorney general at the Department of Justice, denied that it was possible for the FBI to crack DES. "[It is a myth that] we have supercomputers that can crack anything that is out there," Litt said. "Let me put the technical problem in context: It took 14,000 Pentium computers working for four months to decrypt a single message…We are not just talking FBI and NSA [needing massive computing power], we are talking about every police department." (See the full story at http://www.wired.com/news/news/politics/story/12830.html.)
My comment was that the FBI was either incompetent, or lying, or both. No one uses Pentiums to break DES, except as a demonstration. Anyone could have told Litt that.
EFF’s machine is not innovative engineering. It is not state-of-the-art cryptography. It is not cutting-edge technology. The machine uses old, boring chip technologies, simple hardware design, not-very-interesting software, and no cryptography. This is not a marvel of engineering; the only interesting thing is how straightforward the design really is.
Moreover, the machine scales nicely. EFF spent $220,000 on its first machine. They can spend another $220,000, and the double-sized machine will run twice as fast. Now that the basic design work is done, implementation improvements and performance tweaks can increase the performance (or decrease the price) by at least a factor of five. And Moore’s Law predicts that the same machine will be either twice as fast or twice as cheap in another 18 months.
The EFF machine broke DES, but it could just as easily have been designed to break any other encryption algorithm. The attack was against the key length, not against the algorithm design (see http://www.counterpane.com/keylength .html). Moreover, a slightly more expensive design would have used FPGAs, allowing the system to work against a variety of algorithms and algorithm variants.
The only solution here is to pick an algorithm with a longer key. DES has a fixed 56-bit key. Triple-DES has a 112-bit key; there isn’t enough silicon in the galaxy or enough time before the sun burns out to brute force triple-DES. DES-X and XORing additional key blocks before the first round and after the last round add considerable security to DES, and is much cheaper than triple-DES.
The EFF is a civil liberties group, and this was just a demonstration project. Government agencies like the FBI and the NSA would presumably spend a lot more time engineering a more efficient solution. It is reasonable to assume that any country with an intelligence budget has built this sort of machine, probably one a couple of orders of magnitude faster.
There are undoubtedly many, many technical improvements that can be made to the EFF design to make brute-force search cheaper and faster. But the fact that a civil liberties group can use old technology to build something that the administration has denied can be built—that’s the real news.
Sidebar: The AES Candidates
NIST received 15 algorithms in response to its request for AES candidates. They came from companies, universities, and individuals. Ten of the submissions came from outside the U.S.; all but one submission have non-U.S. nationals as at least one coauthor. Three submissions have been broken already, two before the First AES Conference and one during.
Each algorithm has a 128-bit block size, and must support key lengths of 128-, 192, and 256-bits. (Of course, you can always support different key lengths simply by fixing some key bits.) The algorithms will be judged on security (of course), but also speed, flexibility, and simplicity. Speed is speed of encryption and speed of key setup, and is judged on different platforms ranging from high-end microprocessors to 8-bit smart cards to hardware. Flexibility includes suitability to different encryption tasks: encrypting large blocks, changing keys rapidly, fitting into low-powered embedded processors, and the like. Simplicity is the design—simple enough to facilitate analysis.
Here’s a list of the submissions, with a few editorial comments.
- CAST-256. CAST is a family of ciphers designed by Carlisle Adams; as far as I know, none have been broken. This family member (256) is similar to the others. It has a conservative number of rounds, and is slower than some of the other candidates. And the 4 KB of required tables make it difficult to implement in some applications.
- LOKI-97. Like LOKI-89 and LOKI-91, LOKI-97 fell to a differential attack.
- Frog. The algorithm is slow, key setup glacial, and there are many cryptographic problems with the algorithm. A first break was published before the First AES Candidate Conference, and some are extending the attack.
- Mars. IBM gave the world DES, and Mars is its submission to AES. The algorithm is very fast on the Pentium Pro/II, but has some large tables. Still, the pedigree and impressive design document make this a strong candidate despite its "kitchen sink" appearance.
- Magenta. Where do I start? There are so many security problems with this algorithm that it was broken during the question session at the First AES Candidate Conference.
- RC6. This submission, by Ron Rivest and others at RSA Data Security Inc., builds on the success of RC5. It’s the fastest submission on the Pentium Pro/II (22 percent faster than Twofish), but its performance drops by almost a factor of three on Pentium machines. It’s slow on smart cards, and doesn’t fit in smart cards with low RAM. An excellent candidate all the same, with a comprehensive analysis document.
- Decorrelated Fast Cipher (DFC). Serge Vaudenay is an excellent cryptographer, and this is an interesting submission. It uses some radical techniques to provide security in surprisingly few rounds. Performance is mediocre, though; 64-bit multiplies are expensive on most platforms. I’ve heard this called a "research cipher."
- Serpent. It’s pretty hard to find anything wrong with this submission. It’s not the fastest, but that’s only because of its overly conservative design. It works on low-memory smart cards and 32-bit CPUs. And its design team includes two of the most impressive names in cryptanalysis this decade—Eli Biham and Lars Knudsen.
- E2. This is NTT’s submission, another Feistel network. The design document is impressive, and I like this cipher a lot. It’s not as fast as some others, but is likely to be a strong candidate.
- Rijndael. A variant of Square, the chief drawback to this cipher is the difficulty Americans have pronouncing it. Square is a strong algorithm, and Rijndael seems to be a strong variant of it. The designers, Vincent Rijmen and Joan Daemen, know what they are doing.
- DEAL. This is a variant of triple-DES, designed by Lars Knudsen. There has been some cryptanalysis, but it looks strong. I don’t know how credible the idea is for AES, though. Triple-DES already exists as an alternative for those not interested in migrating to AES.
- Hasty Pudding Cipher (HPC). Take everything you can think of, throw it in a cipher, shake well, then add some attitude. "Bizarre" is all that I can say.
- Crypton. Like Rijndael, it is a variant of the Square algorithm. Like Rijndael, it is efficient on a variety of platforms. Unlike Rijndael, it was not developed by the authors of Square, but by a Korean professor. Crypton has some clever design elements, but unfortunately the author is not playing by NIST’s rules; he’s modifying the key schedule after the deadline, changing the design, and so on. I fear that the language and culture barrier will prevent this algorithm from going as far as it could.
- Twofish. Twofish was designed by Bruce Schneier, John Kelsey, Chris Hall, and Niels Ferguson of Counterpane Systems, David Wagner of University of California at Berkeley, and Doug Whiting of Hi/fn Inc. I’ve already said enough about it.
- SAFER+. A member of the SAFER family, designed in part by James Massey, this algorithm was submitted by Cylink. It was designed for 8-bit microprocessors, and is very slow on 32-bit machines. The 256-bit key version is even slower than triple-DES.
Noticeably absent is a submission from the NSA. The word is that the NSA had a submission ready, but that NIST asked them not to submit. NIST would prefer that the NSA help them as an impartial evaluator, not as a combatant. (Skipjack is not an AES candidate because it does not meet NIST’s submission criteria: Both the key length and the block length are too short.)
At this writing, 12 AES candidates remain unbroken. This could easily change by the time you read this. Aside from dedicated attacks against the different algorithms, there is a new development in the cryptanalysis world. Eli Biham, Alix Biryukov, and Adi Shamir invented something called “impossible cryptanalysis,” which they have used profitably against Skipjack. Since none of the AES submissions have been designed with impossible cryptanalysis in mind (with the possible exception of Biham’s own Serpent), it will be interesting to see how they fare.
The NIST web site (http://www.nist.gov/aes/) has discussion groups on the different algorithms, and links to the home pages of the various candidates.
Categories: Twofish